Advanced Cava Demo

This set of examples goes a bit further than Cava's tutorial and showcases some advanced features. For a more gentle introduction or setup instructions, the tutorial is the best place to start.

Here's the high-level overview of what we'll cover:

1. We'll write one circuit template to capture the logical structure of an algorithm, and then show how to instantiate it with different subcircuits in order to perform different computations.
2. We'll construct a circuit that efficiently multiplies by any fixed "compile time" constant by constructing the circuit dynamically according to the constant.
3. We'll prove everything correct in full generality, meaning the proofs apply to any choice of subcircuits/constants/other parameters!

Some pieces of boilerplate code have been omitted for readability of this page. You can view the source on our GitHub repo to see it, or to step through the code locally.

In this demo, we'll define a circuit that executes a classic arithmetic algorithm, exponentiation by squaring (wikipedia). The pseudocode looks like:

exp(x,e):
  if e = 0:
    return 1
  r = exp (x, e // 2)
  if e is even:
    return r^2
  else:
    return r^2 * x

Essentially, you can compute x^e quickly by looking at the bitwise representation of e and either multiplying by x or squaring. This saves operations in comparison to the naive approach, especially for large numbers. To compute x^19, for instance, you would need only 8 multiplications instead of the 18 you would need with a naive approach:

exp(x,19) = exp(x,9) ^ 2 * x
exp(x,9) = exp(x,4) ^ 2 * x
exp(x,4) = exp(x,2) ^ 2
exp(x,2) = exp(x,1) ^ 2
exp(x,1) = exp(x,0) ^ 2 * x
exp(x,0) = 1

If you substitute addition and doubling for multiplication and squaring in this algorithm, and return 0 instead of 1 in the base case, it will compute multiplication instead of exponentiation ("multiplication by doubling"). In this case, you would compute x*19 as:

exp(x,19) = exp(x,9) * 2 + x
exp(x,9) = exp(x,4) * 2 + x
exp(x,4) = exp(x,2) * 2
exp(x,2) = exp(x,1) * 2
exp(x,1) = exp(x,0) * 2 + x
exp(x,0) = 1

For our hardware implementation, we'll assume that x is a fixed constant known before we build the circuit, and that we get the exponent as a stream of bits (most significant bit first). As a circuit diagram, it looks like:

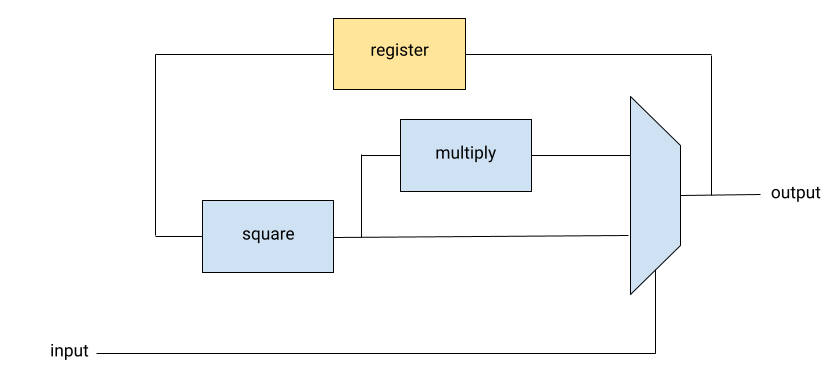
In Cava, this circuit would be defined as follows:

  Definition exp_by_squaring {A} (identity : combType A)
             (square : Circuit (signal A) (signal A))
             (multiply : Circuit (signal A) (signal A))
    : Circuit (signal Bit) (signal A) :=
    LoopInit identity
             ((* start: exp[i], r *)
               Second (square >==> (* r^2 *)
                              Comb fork2 >==> (* r^2, r^2 *)
                              Second multiply (* r^2, r^2*x *))
                      >==> (* exp[i], (r^2, r^2*x) *)
                      Comb (uncurry mux2 >=> fork2) (* r', r' *)).

In order to support both multiplication and exponentiation with the same definition, we haven't specified yet what exactly our "square" and "multiply" procedures are. In Cava, you can take subcircuits as arguments to your circuit definition, much like in some programming languages you can pass functions as arguments to other functions. In pseudocode, this template would be analogous to:

exp(identity, square, multiply, e):
  if e = 0:
    return identity
  r = exp(identity, square, multiply, e // 2)
  r2 = square(r)
  if e is even:
    return r2
  else:
    return multiply(r2)

Note that multiply has only one operand here; since we assume x is a fixed constant, the multiply is already specialized to multiply the input by x.

This circuit is so general that it can actually be adapted for even more purposes than exponentiation and multiplication. By plugging in a no-op for square and an incrementer for multiply, we can simply count the high bits of the input stream:

  (* count the number of high bits in the input stream *)
  Definition count_ones {n}
    : Circuit (signal Bit) (signal (Vec Bit n)) :=
    exp_by_squaring
      (Vec.of_N 0) (Comb ret) (Comb incrN).

We can simulate the circuit to check that it has the desired behavior:

Compute map Bv2N (simulate (count_ones (n:=8))
                           [true;true;true;false;false;true]).
= [1%N; 2%N; 3%N; 3%N; 3%N; 4%N]
: list N

The incrN subcircuit adds 1 to the input bitvector without growing the size of the vector. This component is part of Cava's core library; check out the reference to browse the various verified circuit components that are included. Vec.of_N is also part of this library; it converts a number of Coq's N (binary natural numbers) type into a constant Cava bit-vector.

Next, let's try to define multiplication-by-doubling. We'll need to have subcircuits for addition of a constant and for doubling. For addition, we can use the addN circuit that's included in Cava's standard library. Doubling, however, can be treated as a bitwise operation; we can shift left by one. So let's define a specific double circuit separately:

  (* double a bitvector by adding 0 and truncating *)
  Definition double {n}
    : Circuit (signal (Vec Bit n)) (signal (Vec Bit n)) :=
    Comb (Vec.cons zero >=> Vec.shiftout).

Now, we can write a circuit that, given a constant x, computes x times the input stream:

  (* multiply x by the input stream *)
  Definition stream_multiply {n} (x : N)
    : Circuit (signal Bit) (signal (Vec Bit n)) :=
    (* Circuit that adds x to the input bitvector *)
    let addx := Comb (fun i => addN (i, Vec.of_N x)) in
    exp_by_squaring (Vec.of_N 0) double addx.

Let's simulate it to see if it works. [true;false;false;true] is an input stream that represents the number 9, so this simulation computes 3*9.

(* 3 * 9 = 27 *)
Compute map Bv2N (simulate (stream_multiply (n:=8) 3)
                           [true;false;false;true]).
= [3%N; 6%N; 12%N; 27%N]
: list N

The test becomes more readable if we write a quick helper function to convert numbers into streams:

(* Helper for simulation: convert a number into a list of bits with the most
   significant bit first *)
Definition to_stream (x : N) : list bool :=
  (* reverse because N2Bv puts the least significant bit first *)
  rev (Vector.to_list (N2Bv x)).

(* 3 * 9 = 27 *)
Compute map Bv2N (simulate (stream_multiply (n:=8) 3)
                           (to_stream 9)).
= [3%N; 6%N; 12%N; 27%N]
: list N

(* 5 * 6 = 30 *)
Compute map Bv2N (simulate (stream_multiply (n:=8) 5)
                           (to_stream 6)).
= [5%N; 15%N; 30%N]
: list N

(* 5 * 60 = 300 (bit vector size increased to 16) *)
Compute map Bv2N (simulate (stream_multiply (n:=16) 5)
                           (to_stream 60)).
= [5%N; 15%N; 35%N; 75%N; 150%N; 300%N]
: list N

So far, so good. But how about exponentiation by squaring? Now, we need one subcircuit to multiply by a constant and one subcircuit to square the input. Cava's core library already includes squareN, which squares an input bit-vector and truncates to the input size, so squaring is taken care of.

However, for multiplication, since one of the operands is a constant, it might be efficient to construct our circuit in a way that takes advantage of that fact. In Cava, we can actually write circuits that change structure based on constant arguments. This circuit multiplies its input by the number x, which is expressed as Coq's strictly-positive bitvector type, positive.

  (* construct a circuit to multiply the input by a compile-time
     constant (expressed as a strictly positive Coq bitvector) *)
  Fixpoint mul_const_pos {n} (x : positive)
    : Circuit (signal (Vec Bit n)) (signal (Vec Bit n)) :=
    (match x with
     | 1 => Comb ret
     | y~0 =>
       (* x * i = 2 * y * i *)
       (mul_const_pos y) >==> double
     | y~1 =>
       (* x * i = (2 * y + 1) * i = 2 * y * i + i *)
       Comb fork2 >==> (* i, i *)
            First (mul_const_pos y >==> double) >==> (* 2*y*i, i *)
            Comb addN (* 2*y*i + i *)
     end)%positive.

In case the syntax here is unfamiliar: the match here separates three cases, which correspond to the three constructors of positive. In the first case, x = 1, in which case multiplying by x is just the identity (Comb ret can be read as "a wire"). In the second case, x is constructed from another positive y with a 0 appended to the end, so x = 2*y). In the third case, x is constructed from another positive y, but this time with a 1 appended to the end, so x = 2*y + 1.

We want to handle the case where x = 0 too, so we can define another wrapper function on top where x has the type of Coq's nonnegative bit-vectors, N. N has two constructors; either x is a zero, or x is a positive. So to define our circuit in terms of N, we just produce a circuit that always returns 0 if x is zero and call mul_const_pos to construct the positive case.

  (* construct a circuit to multiply the input by a compile-time
     constant (expressed as a nonnegative Coq bitvector) *)
  Definition mul_constN {n} (x : N)
    : Circuit (signal (Vec Bit n)) (signal (Vec Bit n)) :=
    match x with
    | 0%N => Comb (fun _ => ret (Vec.of_N 0))
    | Npos p => mul_const_pos p
    end.

We can try out constructing this circuit for different values of x to see how it behaves.

Eval cbv [mul_constN mul_const_pos] in mul_constN 1.
= Comb ret
: Circuit (combType (Vec Bit ?n))
    (combType (Vec Bit ?n))
Eval cbv [mul_constN mul_const_pos] in mul_constN 4.
= Comb ret >==> double >==> double
: Circuit (combType (Vec Bit ?n))
    (combType (Vec Bit ?n))
Eval cbv [mul_constN mul_const_pos] in mul_constN 5.
= Comb fork2 >==>
  First (Comb ret >==> double >==> double) >==>
  Comb addN
: Circuit (combType (Vec Bit ?n))
    (combType (Vec Bit ?n))
Eval cbv [mul_constN mul_const_pos] in mul_constN 16.
= Comb ret >==> double >==> double >==> double >==>
  double
: Circuit (combType (Vec Bit ?n))
    (combType (Vec Bit ?n))
Eval cbv [mul_constN mul_const_pos] in mul_constN 20.
= Comb fork2 >==>
  First (Comb ret >==> double >==> double) >==>
  Comb addN >==> double >==> double
: Circuit (combType (Vec Bit ?n))
    (combType (Vec Bit ?n))
Eval cbv [mul_constN mul_const_pos] in mul_constN 2048.
= Comb ret >==> double >==> double >==> double >==>
  double >==> double >==> double >==> double >==>
  double >==> double >==> double >==> double
: Circuit (combType (Vec Bit ?n))
    (combType (Vec Bit ?n))
Eval cbv [mul_constN mul_const_pos] in mul_constN 100000.
= Comb fork2 >==>
  First
    (Comb fork2 >==>
     First
       (Comb fork2 >==>
        First
          (Comb fork2 >==>
           First (... >==> double) >==> Comb addN >==>
           double) >==> Comb addN >==> double >==>
        double) >==> Comb addN >==> double >==>
     double) >==> Comb addN >==> double >==>
  double >==> double >==> double >==> double
: Circuit (combType (Vec Bit ?n))
    (combType (Vec Bit ?n))

Here are the circuit diagrams for some of the smaller ones:

Above: circuit diagram for mul_constN 1.

Above: circuit diagram for mul_constN 4.

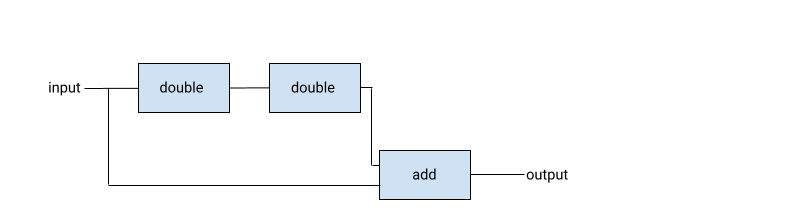
Above: circuit diagram for mul_constN 5.

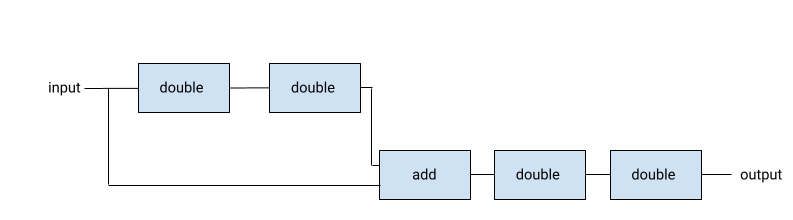
Above: circuit diagram for mul_constN 20. Note that this is the same as composing mul_constN 5 and mul_constN 4.

Now that we can multiply by constants efficiently, we can build a circuit that implements exponentiation by squaring:

  (* raise x to the power of the input stream *)
  Definition stream_exponentiate {n} (x : N)
    : Circuit (signal Bit) (signal (Vec Bit n)) :=
    exp_by_squaring (Vec.of_N 1) (Comb squareN) (mul_constN x).

It works!

(* Compute 3 ^ 5 = 243 *)
Compute map Bv2N
        (simulate (stream_exponentiate (n:=8) 3)
                  (to_stream 5)).
= [3%N; 9%N; 243%N]
: list N

(* Compute 5 ^ 6 = 15625 *)
Compute map Bv2N
        (simulate (stream_exponentiate (n:=16) 5)
                  (to_stream 6)).
= [5%N; 125%N; 15625%N]
: list N

(* Compute 3 ^ 123
   = 48519278097689642681155855396759336072749841943521979872827 *)
Compute map Bv2N
        (simulate (stream_exponentiate (n:=200) 3)
                  (to_stream 123)).
= [3%N; 27%N; 2187%N; 14348907%N;
  205891132094649%N;
  127173474825648610542883299603%N;
  48519278097689642681155855396759336072749841943521979872827%N]
: list N

Now that we've defined all our circuits and tested them a little bit to make sure they work for some inputs, it's time to prove them correct more rigorously. The really cool thing about defining these circuits in Coq is that now we can prove that they behave as expected for all possible inputs. We can even prove that they work for all constant parameters, such as the bit-vector size n for stream_exponentiate and the constant x for mul_constN. In a sense, we're not just proving that our one single circuit is correct; we're proving that the strategy we use to construct it is always correct. This kind of reasoning is an extremely powerful tool.

First, we'll want to prove that exp_by_squaring is correct. We'll define a specification for it in Coq's specification language that captures the crux of the algorithm.

Definition exp_by_squaring_spec
           {A} (mulx square : A -> A)
           (id : A) (exponent : list bool) : A :=
  fold_left
    (fun r (bit : bool) => if bit then mulx (square r) else square r)
    exponent id.

This specification takes a stream of input and produces the output value we expect from the circuit after that stream of input has been processed. But this doesn't quite match our circuit's behavior; we'll get intermediate values as well. We can define a helper function to apply our specification to each prefix of the input:

Definition map_stream {A B} (f : list A -> B) (input : list A) : list B
  := map (fun n => f (firstn (S n) input)) (seq 0 (length input)).

And now, the proof! It more or less comes down to applying a loop-invariant lemma, using the preconditions about square and multiply to rewrite those expressions, and doing some list manipulations. Just like in the tutorial, it's our suggestion to focus more on the proof statements (the part between Lemma and Proof) than the proof bodies (the part between Proof and Qed). The former is intended for humans to read and reason about; the latter is an argument to Coq that the statement is true, and if the Coq typechecker accepts it then the argument must be valid (unless there's a bug in Coq itself).

Lemma exp_by_squaring_correct {A}
      (mul_spec square_spec : combType A -> combType A)
      (identity : combType A)
      (square multiply : Circuit (combType A) (combType A))
      (square_correct :
         forall st i, step square st i = (st, square_spec i))
      (multiply_correct :
         forall st i, step multiply st i = (st, mul_spec i))
      (input : list bool) :
  simulate (exp_by_squaring identity square multiply) input
  = map_stream (exp_by_squaring_spec mul_spec square_spec identity)
               input.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
simulate (exp_by_squaring identity square multiply)
  input =
map_stream
  (exp_by_squaring_spec mul_spec square_spec identity)
  input
Proof.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
simulate (exp_by_squaring identity square multiply)
  input =
map_stream
  (exp_by_squaring_spec mul_spec square_spec identity)
  input
  cbv [exp_by_squaring map_stream].
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
simulate
  (LoopInit identity
     (Second
        (square >==> Comb fork2 >==> Second multiply) >==>
      Comb (uncurry mux2 >=> fork2))) input =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input))
  autorewrite with push_simulate.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
fold_left_accumulate
  (fun '(cs, st) (i : combType Bit) =>
   let
   '(cs', (o, st')) :=
    step
      (Second
         (square >==> Comb fork2 >==> Second multiply) >==>
       Comb (uncurry mux2 >=> fork2)) cs 
      (i, st) in (cs', st', o)) input
  (reset_state
     (Second
        (square >==> Comb fork2 >==> Second multiply) >==>
      Comb (uncurry mux2 >=> fork2)), identity) =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input))

  (* apply loop invariant lemma *)
  eapply fold_left_accumulate_invariant_seq
    with (I:=fun i st out =>
               out = map (fun n => exp_by_squaring_spec
                                  mul_spec square_spec
                                  identity (firstn (S n) input))
                         (seq 0 i)
               /\ snd st = exp_by_squaring_spec
                       mul_spec square_spec identity (firstn i input)).
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
[] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 0) /\
snd
  (reset_state
     (Second
        (square >==> Comb fork2 >==> Second multiply) >==>
      Comb (uncurry mux2 >=> fork2)), identity) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn 0 input)
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
forall (t : nat)
  (st : circuit_state
          (Second
             (square >==> Comb fork2 >==>
              Second multiply) >==>
           Comb (uncurry mux2 >=> fork2)) * 
        combType A) (acc : list (combType A))
  (d : combType Bit),
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) /\
snd st =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn t input) ->
0 <= t < Datatypes.length input ->
let out :=
  (let
   '(cs, st0) := st in
    fun i : combType Bit =>
    let
    '(cs', (o, st')) :=
     step
       (Second
          (square >==> Comb fork2 >==> Second multiply) >==>
        Comb (uncurry mux2 >=> fork2)) cs 
       (i, st0) in (cs', st', o)) 
    (nth t input d) in
acc ++ [snd out] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd (fst out) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input)
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
forall
  (st : circuit_state
          (Second
             (square >==> Comb fork2 >==>
              Second multiply) >==>
           Comb (uncurry mux2 >=> fork2)) * 
        combType A) (acc : list (combType A)),
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input)) /\
snd st =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (Datatypes.length input) input) ->
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input))
  { (* invariant holds in reset state *)
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
[] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 0) /\
snd
  (reset_state
     (Second
        (square >==> Comb fork2 >==> Second multiply) >==>
      Comb (uncurry mux2 >=> fork2)), identity) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn 0 input)
    split; reflexivity. }
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
forall (t : nat)
  (st : circuit_state
          (Second
             (square >==> Comb fork2 >==>
              Second multiply) >==>
           Comb (uncurry mux2 >=> fork2)) * 
        combType A) (acc : list (combType A))
  (d : combType Bit),
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) /\
snd st =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn t input) ->
0 <= t < Datatypes.length input ->
let out :=
  (let
   '(cs, st0) := st in
    fun i : combType Bit =>
    let
    '(cs', (o, st')) :=
     step
       (Second
          (square >==> Comb fork2 >==> Second multiply) >==>
        Comb (uncurry mux2 >=> fork2)) cs 
       (i, st0) in (cs', st', o)) 
    (nth t input d) in
acc ++ [snd out] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd (fst out) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input)
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
forall
  (st : circuit_state
          (Second
             (square >==> Comb fork2 >==>
              Second multiply) >==>
           Comb (uncurry mux2 >=> fork2)) * 
        combType A) (acc : list (combType A)),
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input)) /\
snd st =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (Datatypes.length input) input) ->
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input))
  { (* invariant holds through one timestep *)
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
forall (t : nat)
  (st : circuit_state
          (Second
             (square >==> Comb fork2 >==>
              Second multiply) >==>
           Comb (uncurry mux2 >=> fork2)) * 
        combType A) (acc : list (combType A))
  (d : combType Bit),
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) /\
snd st =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn t input) ->
0 <= t < Datatypes.length input ->
let out :=
  (let
   '(cs, st0) := st in
    fun i : combType Bit =>
    let
    '(cs', (o, st')) :=
     step
       (Second
          (square >==> Comb fork2 >==> Second multiply) >==>
        Comb (uncurry mux2 >=> fork2)) cs 
       (i, st0) in (cs', st', o)) 
    (nth t input d) in
acc ++ [snd out] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd (fst out) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input)
    cbv zeta; intros.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
st:(circuit_state
   (Second
      (square >==> Comb fork2 >==>
       Second multiply) >==>
    Comb (uncurry mux2 >=> fork2)) * 
 combType A)%type
acc:list (combType A)
d:combType Bit
H:acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec
     identity (firstn (S n) input)) 
  (seq 0 t) /\
snd st =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn t input)
H0:0 <= t < Datatypes.length input
acc ++
[snd
   ((let
     '(cs, st) := st in
      fun i : combType Bit =>
      let
      '(cs', (o, st')) :=
       step
         (Second
            (square >==> Comb fork2 >==>
             Second multiply) >==>
          Comb (uncurry mux2 >=> fork2)) cs 
         (i, st) in (cs', st', o)) 
      (nth t input d))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd
  (fst
     ((let
       '(cs, st) := st in
        fun i : combType Bit =>
        let
        '(cs', (o, st')) :=
         step
           (Second
              (square >==> Comb fork2 >==>
               Second multiply) >==>
            Comb (uncurry mux2 >=> fork2)) cs 
           (i, st) in 
         (cs', st', o)) 
        (nth t input d))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input) logical_simplify; subst.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
st:(circuit_state
   (Second
      (square >==> Comb fork2 >==>
       Second multiply) >==>
    Comb (uncurry mux2 >=> fork2)) * 
 combType A)%type
d:combType Bit
H2:snd st =
exp_by_squaring_spec mul_spec square_spec
  identity (firstn t input)
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[snd
   ((let
     '(cs, st) := st in
      fun i : combType Bit =>
      let
      '(cs', (o, st')) :=
       step
         (Second
            (square >==> Comb fork2 >==>
             Second multiply) >==>
          Comb (uncurry mux2 >=> fork2)) cs 
         (i, st) in (cs', st', o)) 
      (nth t input d))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd
  (fst
     ((let
       '(cs, st) := st in
        fun i : combType Bit =>
        let
        '(cs', (o, st')) :=
         step
           (Second
              (square >==> Comb fork2 >==>
               Second multiply) >==>
            Comb (uncurry mux2 >=> fork2)) cs 
           (i, st) in 
         (cs', st', o)) 
        (nth t input d))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input)
    destruct_products.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
c0:combType A
d:combType Bit
H2:snd (c, c0) =
exp_by_squaring_spec mul_spec square_spec
  identity (firstn t input)
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[snd
   (let
    '(cs', (o, st')) :=
     step
       (Second
          (square >==> Comb fork2 >==> Second multiply) >==>
        Comb (uncurry mux2 >=> fork2)) c
       (nth t input d, c0) in 
     (cs', st', o))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd
  (fst
     (let
      '(cs', (o, st')) :=
       step
         (Second
            (square >==> Comb fork2 >==>
             Second multiply) >==>
          Comb (uncurry mux2 >=> fork2)) c
         (nth t input d, c0) in 
       (cs', st', o))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input) cbn [fst snd] in *.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
c0:combType A
d:combType Bit
H2:c0 =
exp_by_squaring_spec mul_spec square_spec
  identity (firstn t input)
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[snd
   (let
    '(cs', (o, st')) :=
     step
       (Second
          (square >==> Comb fork2 >==> Second multiply) >==>
        Comb (uncurry mux2 >=> fork2)) c
       (nth t input d, c0) in 
     (cs', st', o))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd
  (fst
     (let
      '(cs', (o, st')) :=
       step
         (Second
            (square >==> Comb fork2 >==>
             Second multiply) >==>
          Comb (uncurry mux2 >=> fork2)) c
         (nth t input d, c0) in 
       (cs', st', o))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input) subst.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
d:combType Bit
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[snd
   (let
    '(cs', (o, st')) :=
     step
       (Second
          (square >==> Comb fork2 >==> Second multiply) >==>
        Comb (uncurry mux2 >=> fork2)) c
       (nth t input d,
       exp_by_squaring_spec mul_spec square_spec
         identity (firstn t input)) in 
     (cs', st', o))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd
  (fst
     (let
      '(cs', (o, st')) :=
       step
         (Second
            (square >==> Comb fork2 >==>
             Second multiply) >==>
          Comb (uncurry mux2 >=> fork2)) c
         (nth t input d,
         exp_by_squaring_spec mul_spec square_spec
           identity (firstn t input)) in 
       (cs', st', o))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input)
    cbv [mcompose uncurry].
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
d:combType Bit
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[snd
   (let
    '(cs', (o, st')) :=
     step
       (Second
          (square >==> Comb fork2 >==> Second multiply) >==>
        Comb
          (fun
             x : combType Bit *
                 (combType A * combType A) =>
           x <- (let (x0, y) := x in mux2 x0 y);;
           fork2 x)) c
       (nth t input d,
       exp_by_squaring_spec mul_spec square_spec
         identity (firstn t input)) in 
     (cs', st', o))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd
  (fst
     (let
      '(cs', (o, st')) :=
       step
         (Second
            (square >==> Comb fork2 >==>
             Second multiply) >==>
          Comb
            (fun
               x : combType Bit *
                   (combType A * combType A) =>
             x <- (let (x0, y) := x in mux2 x0 y);;
             fork2 x)) c
         (nth t input d,
         exp_by_squaring_spec mul_spec square_spec
           identity (firstn t input)) in 
       (cs', st', o))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input) simpl_ident.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
d:combType Bit
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[snd
   (let
    '(cs', (o, st')) :=
     step
       (Second
          (square >==> Comb fork2 >==> Second multiply) >==>
        Comb
          (fun
             x : combType Bit *
                 (combType A * combType A) =>
           fork2 (let (x0, y) := x in mux2 x0 y))) c
       (nth t input d,
       exp_by_squaring_spec mul_spec square_spec
         identity (firstn t input)) in 
     (cs', st', o))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
snd
  (fst
     (let
      '(cs', (o, st')) :=
       step
         (Second
            (square >==> Comb fork2 >==>
             Second multiply) >==>
          Comb
            (fun
               x : combType Bit *
                   (combType A * combType A) =>
             fork2 (let (x0, y) := x in mux2 x0 y))) c
         (nth t input d,
         exp_by_squaring_spec mul_spec square_spec
           identity (firstn t input)) in 
       (cs', st', o))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input)
    (* simplify step, rewrite with square/multiply correctness lemmas *)
    repeat first [ progress cbn [fst snd step]
                 | rewrite square_correct
                 | rewrite multiply_correct
                 | destruct_pair_let
                 | progress simpl_ident ].
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
d:combType Bit
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[if nth t input d
 then
  mul_spec
    (square_spec
       (exp_by_squaring_spec mul_spec square_spec
          identity (firstn t input)))
 else
  square_spec
    (exp_by_squaring_spec mul_spec square_spec
       identity (firstn t input))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 (S t)) /\
(if nth t input d
 then
  mul_spec
    (square_spec
       (exp_by_squaring_spec mul_spec square_spec
          identity (firstn t input)))
 else
  square_spec
    (exp_by_squaring_spec mul_spec square_spec
       identity (firstn t input))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input)
    (* separate the most recent step from previous steps *)
    autorewrite with pull_snoc natsimpl.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
d:combType Bit
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[if nth t input d
 then
  mul_spec
    (square_spec
       (exp_by_squaring_spec mul_spec square_spec
          identity (firstn t input)))
 else
  square_spec
    (exp_by_squaring_spec mul_spec square_spec
       identity (firstn t input))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[exp_by_squaring_spec mul_spec square_spec identity
   (firstn (S t) input)] /\
(if nth t input d
 then
  mul_spec
    (square_spec
       (exp_by_squaring_spec mul_spec square_spec
          identity (firstn t input)))
 else
  square_spec
    (exp_by_squaring_spec mul_spec square_spec
       identity (firstn t input))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (S t) input)
    rewrite (firstn_succ_snoc input _ ltac:(eassumption))
      by (cbn [combType] in *; lia).
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
d:combType Bit
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[if nth t input d
 then
  mul_spec
    (square_spec
       (exp_by_squaring_spec mul_spec square_spec
          identity (firstn t input)))
 else
  square_spec
    (exp_by_squaring_spec mul_spec square_spec
       identity (firstn t input))] =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input)) 
  (seq 0 t) ++
[exp_by_squaring_spec mul_spec square_spec identity
   (firstn t input ++ [nth t input d])] /\
(if nth t input d
 then
  mul_spec
    (square_spec
       (exp_by_squaring_spec mul_spec square_spec
          identity (firstn t input)))
 else
  square_spec
    (exp_by_squaring_spec mul_spec square_spec
       identity (firstn t input))) =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn t input ++ [nth t input d])
    cbv [exp_by_squaring_spec].
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
d:combType Bit
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   fold_left
     (fun (r : combType A) (bit : bool) =>
      if bit
      then mul_spec (square_spec r)
      else square_spec r) 
     (firstn (S n) input) identity) 
  (seq 0 t) ++
[if nth t input d
 then
  mul_spec
    (square_spec
       (fold_left
          (fun (r : combType A) (bit : bool) =>
           if bit
           then mul_spec (square_spec r)
           else square_spec r) 
          (firstn t input) identity))
 else
  square_spec
    (fold_left
       (fun (r : combType A) (bit : bool) =>
        if bit
        then mul_spec (square_spec r)
        else square_spec r) 
       (firstn t input) identity)] =
map
  (fun n : nat =>
   fold_left
     (fun (r : combType A) (bit : bool) =>
      if bit
      then mul_spec (square_spec r)
      else square_spec r) 
     (firstn (S n) input) identity) 
  (seq 0 t) ++
[fold_left
   (fun (r : combType A) (bit : bool) =>
    if bit
    then mul_spec (square_spec r)
    else square_spec r)
   (firstn t input ++ [nth t input d]) identity] /\
(if nth t input d
 then
  mul_spec
    (square_spec
       (fold_left
          (fun (r : combType A) (bit : bool) =>
           if bit
           then mul_spec (square_spec r)
           else square_spec r) 
          (firstn t input) identity))
 else
  square_spec
    (fold_left
       (fun (r : combType A) (bit : bool) =>
        if bit
        then mul_spec (square_spec r)
        else square_spec r) 
       (firstn t input) identity)) =
fold_left
  (fun (r : combType A) (bit : bool) =>
   if bit
   then mul_spec (square_spec r)
   else square_spec r)
  (firstn t input ++ [nth t input d]) identity
    autorewrite with push_list_fold.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
t:nat
c:circuit_state
  (Second
     (square >==> Comb fork2 >==> Second multiply) >==>
   Comb (uncurry mux2 >=> fork2))
d:combType Bit
H0:0 <= t
H1:t < Datatypes.length input
map
  (fun n : nat =>
   fold_left
     (fun (r : combType A) (bit : bool) =>
      if bit
      then mul_spec (square_spec r)
      else square_spec r) 
     (firstn (S n) input) identity) 
  (seq 0 t) ++
[if nth t input d
 then
  mul_spec
    (square_spec
       (fold_left
          (fun (r : combType A) (bit : bool) =>
           if bit
           then mul_spec (square_spec r)
           else square_spec r) 
          (firstn t input) identity))
 else
  square_spec
    (fold_left
       (fun (r : combType A) (bit : bool) =>
        if bit
        then mul_spec (square_spec r)
        else square_spec r) 
       (firstn t input) identity)] =
map
  (fun n : nat =>
   fold_left
     (fun (r : combType A) (bit : bool) =>
      if bit
      then mul_spec (square_spec r)
      else square_spec r) 
     (firstn (S n) input) identity) 
  (seq 0 t) ++
[if nth t input d
 then
  mul_spec
    (square_spec
       (fold_left
          (fun (r : combType A) (bit : bool) =>
           if bit
           then mul_spec (square_spec r)
           else square_spec r) 
          (firstn t input) identity))
 else
  square_spec
    (fold_left
       (fun (r : combType A) (bit : bool) =>
        if bit
        then mul_spec (square_spec r)
        else square_spec r) 
       (firstn t input) identity)] /\
(if nth t input d
 then
  mul_spec
    (square_spec
       (fold_left
          (fun (r : combType A) (bit : bool) =>
           if bit
           then mul_spec (square_spec r)
           else square_spec r) 
          (firstn t input) identity))
 else
  square_spec
    (fold_left
       (fun (r : combType A) (bit : bool) =>
        if bit
        then mul_spec (square_spec r)
        else square_spec r) 
       (firstn t input) identity)) =
(if nth t input d
 then
  mul_spec
    (square_spec
       (fold_left
          (fun (r : combType A) (bit : bool) =>
           if bit
           then mul_spec (square_spec r)
           else square_spec r) 
          (firstn t input) identity))
 else
  square_spec
    (fold_left
       (fun (r : combType A) (bit : bool) =>
        if bit
        then mul_spec (square_spec r)
        else square_spec r) 
       (firstn t input) identity))
    split; reflexivity. }
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
forall
  (st : circuit_state
          (Second
             (square >==> Comb fork2 >==>
              Second multiply) >==>
           Comb (uncurry mux2 >=> fork2)) * 
        combType A) (acc : list (combType A)),
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input)) /\
snd st =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (Datatypes.length input) input) ->
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input))
  { (* invariant implies postcondition *)
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
forall
  (st : circuit_state
          (Second
             (square >==> Comb fork2 >==>
              Second multiply) >==>
           Comb (uncurry mux2 >=> fork2)) * 
        combType A) (acc : list (combType A)),
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input)) /\
snd st =
exp_by_squaring_spec mul_spec square_spec identity
  (firstn (Datatypes.length input) input) ->
acc =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input))
    intros; logical_simplify; subst.
A:SignalType
mul_spec, square_spec:combType A -> combType A
identity:combType A
square, multiply:Circuit (combType A) (combType A)
square_correct:forall (st : circuit_state square)
  (i : combType A),
step square st i =
(st, square_spec i)
multiply_correct:forall
  (st : circuit_state multiply)
  (i : combType A),
step multiply st i =
(st, mul_spec i)
input:list bool
st:(circuit_state
   (Second
      (square >==> Comb fork2 >==>
       Second multiply) >==>
    Comb (uncurry mux2 >=> fork2)) * 
 combType A)%type
H0:snd st =
exp_by_squaring_spec mul_spec square_spec
  identity
  (firstn (Datatypes.length input) input)
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input)) =
map
  (fun n : nat =>
   exp_by_squaring_spec mul_spec square_spec identity
     (firstn (S n) input))
  (seq 0 (Datatypes.length input)) reflexivity. }
Qed.

From here, we no longer have to reason about the exponentiation-by-squaring circuit; we can use this lemma to prove all our other circuits are correct. Instead, we can reason about exp_by_squaring_spec, with no circuit-related reasoning. For example, to prove the count_ones circuit correct, we first prove that our specification (which is based on the Coq standard library definition count_occ) matches exp_by_squaring_spec.

(* helper lemma proving that count_occ is a specialization of
   exp_by_squaring_spec *)
Lemma count_occ_is_exp_by_squaring n l start :
  exp_by_squaring_spec
    (A:=combType (Vec Bit n))
    (fun v => N2Bv_sized n (Bv2N v + 1)) (fun v => v)
    (N2Bv_sized n start) l
  = N2Bv_sized n (N.of_nat (count_occ bool_dec l true) + start).
n:nat
l:list bool
start:N
exp_by_squaring_spec
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + 1))
  (fun v : combType (Vec Bit n) => v)
  (N2Bv_sized n start) l =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start)
Proof.
n:nat
l:list bool
start:N
exp_by_squaring_spec
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + 1))
  (fun v : combType (Vec Bit n) => v)
  (N2Bv_sized n start) l =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start)
  cbv [exp_by_squaring_spec].
n:nat
l:list bool
start:N
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r) l
  (N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start) revert start.
n:nat
l:list bool
forall start : N,
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r) l
  (N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start)
  induction l as [|bit l]; [ reflexivity | ].
n:nat
bit:bool
l:list bool
IHl:forall start : N,
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r)
  l (N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start)
forall start : N,
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r)
  (bit :: l) (N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec (bit :: l) true) +
   start)
  intros; cbn [count_occ fold_left].
n:nat
bit:bool
l:list bool
IHl:forall start : N,
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r)
  l (N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start)
start:N
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r) l
  (if bit
   then N2Bv_sized n (Bv2N (N2Bv_sized n start) + 1)
   else N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat
     (if bool_dec bit true
      then S (count_occ bool_dec l true)
      else count_occ bool_dec l true) + start)
  destruct bit; destruct_one_match; try congruence; [ ].
n:nat
l:list bool
IHl:forall start : N,
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r)
  l (N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start)
start:N
e:true = true
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r) l
  (N2Bv_sized n (Bv2N (N2Bv_sized n start) + 1)) =
N2Bv_sized n
  (N.of_nat (S (count_occ bool_dec l true)) + start)
  rewrite N2Bv_sized_add_idemp_l.
n:nat
l:list bool
IHl:forall start : N,
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r)
  l (N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start)
start:N
e:true = true
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r) l
  (N2Bv_sized n (start + 1)) =
N2Bv_sized n
  (N.of_nat (S (count_occ bool_dec l true)) + start)
  rewrite IHl.
n:nat
l:list bool
IHl:forall start : N,
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r)
  l (N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start)
start:N
e:true = true
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + (start + 1)) =
N2Bv_sized n
  (N.of_nat (S (count_occ bool_dec l true)) + start) f_equal.
n:nat
l:list bool
IHl:forall start : N,
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit then N2Bv_sized n (Bv2N r + 1) else r)
  l (N2Bv_sized n start) =
N2Bv_sized n
  (N.of_nat (count_occ bool_dec l true) + start)
start:N
e:true = true
(N.of_nat (count_occ bool_dec l true) + (start + 1))%N =
(N.of_nat (S (count_occ bool_dec l true)) + start)%N lia.
Qed.

We can use this lemma to prove that, no matter how many timesteps we run or how big our bit-vector is, the nth output of count_ones will be the number of true values that appear in the first n bits of input, truncated to fit the bit-vector size. Because we're doing all of this with inductive reasoning, it's not at all computationally intensive to write such a proof.

Lemma count_ones_correct n (input : list bool) :
  simulate (count_ones (n:=n)) input
  = map_stream
      (fun l => let count := count_occ bool_dec l true in
             N2Bv_sized n (N.of_nat count))
      input.
n:nat
input:list bool
simulate count_ones input =
map_stream
  (fun l : list bool =>
   let count := count_occ bool_dec l true in
   N2Bv_sized n (N.of_nat count)) input
Proof.
n:nat
input:list bool
simulate count_ones input =
map_stream
  (fun l : list bool =>
   let count := count_occ bool_dec l true in
   N2Bv_sized n (N.of_nat count)) input
  intros; cbv [count_ones].
n:nat
input:list bool
simulate
  (exp_by_squaring (Vec.of_N 0) 
     (Comb ret) (Comb incrN)) input =
map_stream
  (fun l : list bool =>
   N2Bv_sized n (N.of_nat (count_occ bool_dec l true)))
  input
  rewrite exp_by_squaring_correct
    with (mul_spec:=fun v => N2Bv_sized n (Bv2N v + 1))
         (square_spec := fun v : combType (Vec Bit n) => v)
    by (cbn [circuit_state step]; intros;
        lazymatch goal with x : unit |- _ => destruct x end;
        simpl_ident; reflexivity).
n:nat
input:list bool
map_stream
  (exp_by_squaring_spec
     (fun v : Bvector n => N2Bv_sized n (Bv2N v + 1))
     (fun v : combType (Vec Bit n) => v) 
     (Vec.of_N 0)) input =
map_stream
  (fun l : list bool =>
   N2Bv_sized n (N.of_nat (count_occ bool_dec l true)))
  input
  apply map_ext; intros.
n:nat
input:list bool
a:nat
exp_by_squaring_spec
  (fun v : Bvector n => N2Bv_sized n (Bv2N v + 1))
  (fun v : combType (Vec Bit n) => v) 
  (Vec.of_N 0) (firstn (S a) input) =
N2Bv_sized n
  (N.of_nat
     (count_occ bool_dec (firstn (S a) input) true)) simpl_ident.
n:nat
input:list bool
a:nat
exp_by_squaring_spec
  (fun v : Bvector n => N2Bv_sized n (Bv2N v + 1))
  (fun v : combType (Vec Bit n) => v) 
  (N2Bv_sized n 0) (firstn (S a) input) =
N2Bv_sized n
  (N.of_nat
     (count_occ bool_dec (firstn (S a) input) true))
  rewrite count_occ_is_exp_by_squaring.
n:nat
input:list bool
a:nat
N2Bv_sized n
  (N.of_nat
     (count_occ bool_dec (firstn (S a) input) true) +
   0) =
N2Bv_sized n
  (N.of_nat
     (count_occ bool_dec (firstn (S a) input) true))
  f_equal; lia.
Qed.

To prove that stream_multiply is correct, we'll first have to prove the single-step behavior of double (to satisfy the square_correct precondition of exp_by_squaring_correct). That proof is pretty quick:

Lemma double_step n st i :
  step double st i = (st, N2Bv_sized n (Bv2N i + Bv2N i)).
n:nat
st:circuit_state double
i:combType (Vec Bit n)
step double st i =
(st, N2Bv_sized n (Bv2N i + Bv2N i))
Proof.
n:nat
st:circuit_state double
i:combType (Vec Bit n)
step double st i =
(st, N2Bv_sized n (Bv2N i + Bv2N i))
  cbv [double step mcompose].
n:nat
st:circuit_state double
i:combType (Vec Bit n)
(tt, x <- Vec.cons zero i;; Vec.shiftout x) =
(st, N2Bv_sized n (Bv2N i + Bv2N i))
  simpl_ident.
n:nat
st:circuit_state double
i:combType (Vec Bit n)
(tt, Vector.shiftout (false :: i)) =
(st, N2Bv_sized n (Bv2N i + Bv2N i)) rewrite shiftout_cons0.
n:nat
st:circuit_state double
i:combType (Vec Bit n)
(tt, N2Bv_sized n (2 * Bv2N i)) =
(st, N2Bv_sized n (Bv2N i + Bv2N i))
  apply f_equal2; [ destruct st; reflexivity | ].
n:nat
st:circuit_state double
i:combType (Vec Bit n)
N2Bv_sized n (2 * Bv2N i) =
N2Bv_sized n (Bv2N i + Bv2N i)
  f_equal.
n:nat
st:circuit_state double
i:combType (Vec Bit n)
(2 * Bv2N i)%N = (Bv2N i + Bv2N i)%N lia.
Qed.

It's useful to write the inverse operation of to_stream so that we can talk about the numeric value that the input represents:

Definition from_stream (l : list bool) : N :=
  Bv2N (Vector.of_list (rev l)).

Lemma from_stream_cons bit l :
  from_stream (bit :: l)
  = ((if bit then 2 ^ (N.of_nat (length l)) else 0)
     + from_stream l)%N.
bit:bool
l:list bool
from_stream (bit :: l) =
((if bit then 2 ^ N.of_nat (Datatypes.length l) else 0) +
 from_stream l)%N
Proof.
bit:bool
l:list bool
from_stream (bit :: l) =
((if bit then 2 ^ N.of_nat (Datatypes.length l) else 0) +
 from_stream l)%N
  cbv [from_stream].
bit:bool
l:list bool
Bv2N (Vector.of_list (rev (bit :: l))) =
((if bit then 2 ^ N.of_nat (Datatypes.length l) else 0) +
 Bv2N (Vector.of_list (rev l)))%N cbn [rev].
bit:bool
l:list bool
Bv2N (Vector.of_list (rev l ++ [bit])) =
((if bit then 2 ^ N.of_nat (Datatypes.length l) else 0) +
 Bv2N (Vector.of_list (rev l)))%N
  rewrite of_list_snoc.
bit:bool
l:list bool
Bv2N
  (resize_default bit
     (Datatypes.length (rev l ++ [bit]))
     (Vector.of_list (rev l) ++ [bit]%vector)) =
((if bit then 2 ^ N.of_nat (Datatypes.length l) else 0) +
 Bv2N (Vector.of_list (rev l)))%N
  rewrite app_length; cbn [length].
bit:bool
l:list bool
Bv2N
  (resize_default bit (Datatypes.length (rev l) + 1)
     (Vector.of_list (rev l) ++ [bit]%vector)) =
((if bit then 2 ^ N.of_nat (Datatypes.length l) else 0) +
 Bv2N (Vector.of_list (rev l)))%N
  rewrite resize_default_id.
bit:bool
l:list bool
Bv2N (Vector.of_list (rev l) ++ [bit])%vector =
((if bit then 2 ^ N.of_nat (Datatypes.length l) else 0) +
 Bv2N (Vector.of_list (rev l)))%N
  rewrite Bv2N_snoc.
bit:bool
l:list bool
((if bit
  then 2 ^ N.of_nat (Datatypes.length (rev l))
  else 0) + Bv2N (Vector.of_list (rev l)))%N =
((if bit then 2 ^ N.of_nat (Datatypes.length l) else 0) +
 Bv2N (Vector.of_list (rev l)))%N
  f_equal.
bit:bool
l:list bool
(if bit
 then (2 ^ N.of_nat (Datatypes.length (rev l)))%N
 else 0%N) =
(if bit
 then (2 ^ N.of_nat (Datatypes.length l))%N
 else 0%N)
  autorewrite with push_length;
    reflexivity.
Qed.

Now, just like for count_ones, we prove that exp_by_squaring_spec corresponds to multiplication when given the right parameters. We do it in two steps, because for the inductive logic to work out we have to reason about the behavior of exp_by_squaring_spec for any starting value, not just 0.

Lemma multiply_is_exp_by_squaring' n x l start :
  exp_by_squaring_spec
    (A:=combType (Vec Bit n))
    (fun v => N2Bv_sized n (Bv2N v + x))
    (fun v => N2Bv_sized n (Bv2N v + Bv2N v))
    start l
  = N2Bv_sized n (Bv2N start * 2 ^ N.of_nat (length l)
                  + x * from_stream l).
n:nat
x:N
l:list bool
start:combType (Vec Bit n)
exp_by_squaring_spec
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + x))
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + Bv2N v)) start l =
N2Bv_sized n
  (Bv2N start * 2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
Proof.
n:nat
x:N
l:list bool
start:combType (Vec Bit n)
exp_by_squaring_spec
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + x))
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + Bv2N v)) start l =
N2Bv_sized n
  (Bv2N start * 2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
  cbv [exp_by_squaring_spec].
n:nat
x:N
l:list bool
start:combType (Vec Bit n)
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start * 2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
  revert start; induction l.
n:nat
x:N
forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) [] start =
N2Bv_sized n
  (Bv2N start * 2 ^ N.of_nat (Datatypes.length []) +
   x * from_stream [])
n:nat
x:N
a:bool
l:list bool
IHl:forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) 
  (a :: l) start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length (a :: l)) +
   x * from_stream (a :: l))
  {
n:nat
x:N
forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) [] start =
N2Bv_sized n
  (Bv2N start * 2 ^ N.of_nat (Datatypes.length []) +
   x * from_stream []) intros; cbn.
n:nat
x:N
start:combType (Vec Bit n)
start = N2Bv_sized n (Bv2N start * 1 + x * 0)
    rewrite N.mul_0_r, N.add_0_r, N.mul_1_r.
n:nat
x:N
start:combType (Vec Bit n)
start = N2Bv_sized n (Bv2N start)
    rewrite N2Bv_sized_Bv2N; reflexivity. }
n:nat
x:N
a:bool
l:list bool
IHl:forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) 
  (a :: l) start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length (a :: l)) +
   x * from_stream (a :: l))
  {
n:nat
x:N
a:bool
l:list bool
IHl:forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) 
  (a :: l) start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length (a :: l)) +
   x * from_stream (a :: l)) intros.
n:nat
x:N
a:bool
l:list bool
IHl:forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
start:combType (Vec Bit n)
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) 
  (a :: l) start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length (a :: l)) +
   x * from_stream (a :: l)) cbn [fold_left].
n:nat
x:N
a:bool
l:list bool
IHl:forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
start:combType (Vec Bit n)
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool) =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l
  (if a
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N start + Bv2N start)) +
       x)
   else N2Bv_sized n (Bv2N start + Bv2N start)) =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length (a :: l)) +
   x * from_stream (a :: l)) rewrite IHl.
n:nat
x:N
a:bool
l:list bool
IHl:forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
start:combType (Vec Bit n)
N2Bv_sized n
  (Bv2N
     (if a
      then
       N2Bv_sized n
         (Bv2N
            (N2Bv_sized n (Bv2N start + Bv2N start)) +
          x)
      else N2Bv_sized n (Bv2N start + Bv2N start)) *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l) =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length (a :: l)) +
   x * from_stream (a :: l))
    rewrite from_stream_cons.
n:nat
x:N
a:bool
l:list bool
IHl:forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
start:combType (Vec Bit n)
N2Bv_sized n
  (Bv2N
     (if a
      then
       N2Bv_sized n
         (Bv2N
            (N2Bv_sized n (Bv2N start + Bv2N start)) +
          x)
      else N2Bv_sized n (Bv2N start + Bv2N start)) *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l) =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length (a :: l)) +
   x *
   ((if a
     then (2 ^ N.of_nat (Datatypes.length l))%N
     else 0%N) + from_stream l))
    cbn [length].
n:nat
x:N
a:bool
l:list bool
IHl:forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
start:combType (Vec Bit n)
N2Bv_sized n
  (Bv2N
     (if a
      then
       N2Bv_sized n
         (Bv2N
            (N2Bv_sized n (Bv2N start + Bv2N start)) +
          x)
      else N2Bv_sized n (Bv2N start + Bv2N start)) *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l) =
N2Bv_sized n
  (Bv2N start * 2 ^ N.of_nat (S (Datatypes.length l)) +
   x *
   ((if a
     then (2 ^ N.of_nat (Datatypes.length l))%N
     else 0%N) + from_stream l)) rewrite Nat2N.inj_succ, N.pow_succ_r'.
n:nat
x:N
a:bool
l:list bool
IHl:forall start : combType (Vec Bit n),
fold_left
  (fun (r : combType (Vec Bit n)) (bit : bool)
   =>
   if bit
   then
    N2Bv_sized n
      (Bv2N (N2Bv_sized n (Bv2N r + Bv2N r)) + x)
   else N2Bv_sized n (Bv2N r + Bv2N r)) l start =
N2Bv_sized n
  (Bv2N start *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l)
start:combType (Vec Bit n)
N2Bv_sized n
  (Bv2N
     (if a
      then
       N2Bv_sized n
         (Bv2N
            (N2Bv_sized n (Bv2N start + Bv2N start)) +
          x)
      else N2Bv_sized n (Bv2N start + Bv2N start)) *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l) =
N2Bv_sized n
  (Bv2N start *
   (2 * 2 ^ N.of_nat (Datatypes.length l)) +
   x *
   ((if a
     then (2 ^ N.of_nat (Datatypes.length l))%N
     else 0%N) + from_stream l))
    destruct_one_match;
      autorewrite with pull_N2Bv_sized;
      lazymatch goal with
      | |- context [N2Bv_sized n (Bv2N (N2Bv_sized n ?x) * ?y + ?z)] =>
        rewrite <-(N2Bv_sized_add_idemp_l _ _ z);
          autorewrite with pull_N2Bv_sized
      end;
      apply f_equal; lia. }
Qed.

Lemma multiply_is_exp_by_squaring n x l :
  exp_by_squaring_spec
    (A:=combType (Vec Bit n))
    (fun v => N2Bv_sized n (Bv2N v + x))
    (fun v => N2Bv_sized n (Bv2N v + Bv2N v))
    (N2Bv_sized n 0) l
  = N2Bv_sized n (x * from_stream l).
n:nat
x:N
l:list bool
exp_by_squaring_spec
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + x))
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + Bv2N v)) (N2Bv_sized n 0) l =
N2Bv_sized n (x * from_stream l)
Proof.
n:nat
x:N
l:list bool
exp_by_squaring_spec
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + x))
  (fun v : combType (Vec Bit n) =>
   N2Bv_sized n (Bv2N v + Bv2N v)) (N2Bv_sized n 0) l =
N2Bv_sized n (x * from_stream l)
  rewrite multiply_is_exp_by_squaring'.
n:nat
x:N
l:list bool
N2Bv_sized n
  (Bv2N (N2Bv_sized n 0) *
   2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l) =
N2Bv_sized n (x * from_stream l)
  rewrite Bv2N_N2Bv_sized_modulo, N.mod_0_l
    by (apply N.pow_nonzero; lia).
n:nat
x:N
l:list bool
N2Bv_sized n
  (0 * 2 ^ N.of_nat (Datatypes.length l) +
   x * from_stream l) =
N2Bv_sized n (x * from_stream l)
  f_equal; lia.
Qed.

With that, we have all we need to prove stream_multiply is always correct!

Lemma stream_multiply_correct n x (input : list bool) :
  simulate (stream_multiply (n:=n) x) input
  = map_stream
      (fun i => N2Bv_sized n (x * (from_stream i)))
      input.
n:nat
x:N
input:list bool
simulate (stream_multiply x) input =
map_stream
  (fun i : list bool =>
   N2Bv_sized n (x * from_stream i)) input
Proof.
n:nat
x:N
input:list bool
simulate (stream_multiply x) input =
map_stream
  (fun i : list bool =>
   N2Bv_sized n (x * from_stream i)) input
  intros; cbv [stream_multiply].
n:nat
x:N
input:list bool
simulate
  (exp_by_squaring (Vec.of_N 0) double
     (Comb
        (fun i : combType (Vec Bit n) =>
         addN (i, Vec.of_N x)))) input =
map_stream
  (fun i : list bool =>
   N2Bv_sized n (x * from_stream i)) input
  rewrite @exp_by_squaring_correct
    with (A:=Vec Bit n)
         (mul_spec:=fun v => N2Bv_sized n (Bv2N v + x))
         (square_spec := fun v => N2Bv_sized n (Bv2N v + Bv2N v))
    by first [ solve [apply double_step]
             | cbn [circuit_state step]; intros; simpl_ident;
               lazymatch goal with x : unit |- _ => destruct x end;
               rewrite N2Bv_sized_add_idemp_r; reflexivity ].
n:nat
x:N
input:list bool
map_stream
  (exp_by_squaring_spec
     (fun v : Bvector n => N2Bv_sized n (Bv2N v + x))
     (fun v : Bvector n =>
      N2Bv_sized n (Bv2N v + Bv2N v)) 
     (Vec.of_N 0)) input =
map_stream
  (fun i : list bool =>
   N2Bv_sized n (x * from_stream i)) input
  apply map_ext; intros.
n:nat
x:N
input:list bool
a:nat
exp_by_squaring_spec
  (fun v : Bvector n => N2Bv_sized n (Bv2N v + x))
  (fun v : Bvector n => N2Bv_sized n (Bv2N v + Bv2N v))
  (Vec.of_N 0) (firstn (S a) input) =
N2Bv_sized n (x * from_stream (firstn (S a) input)) simpl_ident.
n:nat
x:N
input:list bool
a:nat
exp_by_squaring_spec
  (fun v : Bvector n => N2Bv_sized n (Bv2N v + x))
  (fun v : Bvector n => N2Bv_sized n (Bv2N v + Bv2N v))
  (N2Bv_sized n 0) (firstn (S a) input) =
N2Bv_sized n (x * from_stream (firstn (S a) input))
  apply multiply_is_exp_by_squaring.
Qed.

Now, let's move on to stream_exponentiate. We'll need to prove that mul_constN is correct first, and to prove that we'll need a proof for mul_const_pos. This proof goes by induction on x:

Lemma mul_const_pos_step n x st i :
  step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * Npos x)).
n:nat
x:positive
st:circuit_state (mul_const_pos x)
i:combType (Vec Bit n)
step (mul_const_pos x) st i =
(st, N2Bv_sized n (Bv2N i * N.pos x))
Proof.
n:nat
x:positive
st:circuit_state (mul_const_pos x)
i:combType (Vec Bit n)
step (mul_const_pos x) st i =
(st, N2Bv_sized n (Bv2N i * N.pos x))
  revert st i.
n:nat
x:positive
forall (st : circuit_state (mul_const_pos x))
  (i : combType (Vec Bit n)),
step (mul_const_pos x) st i =
(st, N2Bv_sized n (Bv2N i * N.pos x))
  induction x; cbn [mul_const_pos circuit_state];
    intros; destruct_products;
    repeat lazymatch goal with x : unit |- _ => destruct x end.
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
step
  (Comb fork2 >==> First (mul_const_pos x >==> double) >==>
   Comb addN) (tt, (c, c0), tt) i =
(tt, (c, c0), tt, N2Bv_sized n (Bv2N i * N.pos x~1))
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
step (mul_const_pos x >==> double) (c, c0) i =
(c, c0, N2Bv_sized n (Bv2N i * N.pos x~0))
n:nat
i:combType (Vec Bit n)
step (Comb ret) tt i = (tt, N2Bv_sized n (Bv2N i * 1))
  { (* x = y~1 *)
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
step
  (Comb fork2 >==> First (mul_const_pos x >==> double) >==>
   Comb addN) (tt, (c, c0), tt) i =
(tt, (c, c0), tt, N2Bv_sized n (Bv2N i * N.pos x~1))
    cbn [step].
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(let
 '(cs1, x0) :=
  let
  '(cs2, y) :=
   let
   '(cs', x0) :=
    let
    '(cs1, x0) :=
     step (mul_const_pos x)
       (fst (snd (fst (tt, (c, c0), tt))))
       (fst (fork2 i)) in
     let
     '(cs2, y) :=
      step double (snd (snd (fst (tt, (c, c0), tt))))
        x0 in (cs1, cs2, y) in
    (cs', (x0, snd (fork2 i))) in (tt, cs2, y) in
  (cs1, tt, addN x0)) =
(tt, (c, c0), tt, N2Bv_sized n (Bv2N i * N.pos x~1)) repeat (destruct_pair_let; cbn [fst snd]).
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(tt,
(fst (step (mul_const_pos x) c (fst (fork2 i))),
fst
  (step double c0
     (snd (step (mul_const_pos x) c (fst (fork2 i)))))),
tt,
addN
  (snd
     (step double c0
        (snd
           (step (mul_const_pos x) c (fst (fork2 i))))),
  snd (fork2 i))) =
(tt, (c, c0), tt, N2Bv_sized n (Bv2N i * N.pos x~1))
    simpl_ident.
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(tt,
(fst (step (mul_const_pos x) c i),
fst
  (step double c0 (snd (step (mul_const_pos x) c i)))),
tt,
N2Bv_sized n
  (Bv2N
     (snd
        (step double c0
           (snd (step (mul_const_pos x) c i)))) +
   Bv2N i)) =
(tt, (c, c0), tt, N2Bv_sized n (Bv2N i * N.pos x~1)) rewrite double_step, IHx.
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(tt,
(fst (c, N2Bv_sized n (Bv2N i * N.pos x)),
fst
  (c0,
  N2Bv_sized n
    (Bv2N (snd (c, N2Bv_sized n (Bv2N i * N.pos x))) +
     Bv2N (snd (c, N2Bv_sized n (Bv2N i * N.pos x)))))),
tt,
N2Bv_sized n
  (Bv2N
     (snd
        (c0,
        N2Bv_sized n
          (Bv2N
             (snd (c, N2Bv_sized n (Bv2N i * N.pos x))) +
           Bv2N
             (snd (c, N2Bv_sized n (Bv2N i * N.pos x)))))) +
   Bv2N i)) =
(tt, (c, c0), tt, N2Bv_sized n (Bv2N i * N.pos x~1)) cbn [fst snd].
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(tt, (c, c0), tt,
N2Bv_sized n
  (Bv2N
     (N2Bv_sized n
        (Bv2N (N2Bv_sized n (Bv2N i * N.pos x)) +
         Bv2N (N2Bv_sized n (Bv2N i * N.pos x)))) +
   Bv2N i)) =
(tt, (c, c0), tt, N2Bv_sized n (Bv2N i * N.pos x~1))
    f_equal; [ ].
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
N2Bv_sized n
  (Bv2N
     (N2Bv_sized n
        (Bv2N (N2Bv_sized n (Bv2N i * N.pos x)) +
         Bv2N (N2Bv_sized n (Bv2N i * N.pos x)))) +
   Bv2N i) = N2Bv_sized n (Bv2N i * N.pos x~1)
    autorewrite with pull_N2Bv_sized.
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
N2Bv_sized n
  (Bv2N (N2Bv_sized n (Bv2N i * N.pos x)) +
   Bv2N (N2Bv_sized n (Bv2N i * N.pos x)) + Bv2N i) =
N2Bv_sized n (Bv2N i * N.pos x~1)
    repeat lazymatch goal with
           | |- context
                 [N2Bv_sized n (Bv2N (N2Bv_sized n ?x) + ?y + ?z)] =>
             replace (Bv2N (N2Bv_sized n x) + y + z)%N
               with (y + z + Bv2N (N2Bv_sized n x))%N by lia;
               autorewrite with pull_N2Bv_sized
           end.
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
N2Bv_sized n
  (Bv2N i + Bv2N i * N.pos x + Bv2N i * N.pos x) =
N2Bv_sized n (Bv2N i * N.pos x~1)
    f_equal; lia. }
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
step (mul_const_pos x >==> double) (c, c0) i =
(c, c0, N2Bv_sized n (Bv2N i * N.pos x~0))
n:nat
i:combType (Vec Bit n)
step (Comb ret) tt i = (tt, N2Bv_sized n (Bv2N i * 1))
  { (* x = y~0 *)
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
step (mul_const_pos x >==> double) (c, c0) i =
(c, c0, N2Bv_sized n (Bv2N i * N.pos x~0))
    cbn [step].
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(let
 '(cs1, x0) := step (mul_const_pos x) (fst (c, c0)) i
  in
  let
  '(cs2, y) := step double (snd (c, c0)) x0 in
   (cs1, cs2, y)) =
(c, c0, N2Bv_sized n (Bv2N i * N.pos x~0)) repeat (destruct_pair_let; cbn [fst snd]).
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(fst (step (mul_const_pos x) c i),
fst
  (step double c0 (snd (step (mul_const_pos x) c i))),
snd
  (step double c0 (snd (step (mul_const_pos x) c i)))) =
(c, c0, N2Bv_sized n (Bv2N i * N.pos x~0))
    simpl_ident.
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(fst (step (mul_const_pos x) c i),
fst
  (step double c0 (snd (step (mul_const_pos x) c i))),
snd
  (step double c0 (snd (step (mul_const_pos x) c i)))) =
(c, c0, N2Bv_sized n (Bv2N i * N.pos x~0)) rewrite double_step, IHx.
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(fst (c, N2Bv_sized n (Bv2N i * N.pos x)),
fst
  (c0,
  N2Bv_sized n
    (Bv2N (snd (c, N2Bv_sized n (Bv2N i * N.pos x))) +
     Bv2N (snd (c, N2Bv_sized n (Bv2N i * N.pos x))))),
snd
  (c0,
  N2Bv_sized n
    (Bv2N (snd (c, N2Bv_sized n (Bv2N i * N.pos x))) +
     Bv2N (snd (c, N2Bv_sized n (Bv2N i * N.pos x)))))) =
(c, c0, N2Bv_sized n (Bv2N i * N.pos x~0)) cbn [fst snd].
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
(c, c0,
N2Bv_sized n
  (Bv2N (N2Bv_sized n (Bv2N i * N.pos x)) +
   Bv2N (N2Bv_sized n (Bv2N i * N.pos x)))) =
(c, c0, N2Bv_sized n (Bv2N i * N.pos x~0))
    f_equal; [ ].
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
N2Bv_sized n
  (Bv2N (N2Bv_sized n (Bv2N i * N.pos x)) +
   Bv2N (N2Bv_sized n (Bv2N i * N.pos x))) =
N2Bv_sized n (Bv2N i * N.pos x~0)
    autorewrite with pull_N2Bv_sized.
n:nat
x:positive
IHx:forall (st : circuit_state (mul_const_pos x)) (i : combType (Vec Bit n)),
step (mul_const_pos x) st i = (st, N2Bv_sized n (Bv2N i * N.pos x))
c:circuit_state (mul_const_pos x)
c0:circuit_state double
i:combType (Vec Bit n)
N2Bv_sized n (Bv2N i * N.pos x + Bv2N i * N.pos x) =
N2Bv_sized n (Bv2N i * N.pos x~0)
    f_equal; lia. }
n:nat
i:combType (Vec Bit n)
step (Comb ret) tt i = (tt, N2Bv_sized n (Bv2N i * 1))
  { (* x = 1 *)
n:nat
i:combType (Vec Bit n)
step (Comb ret) tt i = (tt, N2Bv_sized n (Bv2N i * 1))
    cbn [step].
n:nat
i:combType (Vec Bit n)
(tt, ret i) = (tt, N2Bv_sized n (Bv2N i * 1)) simpl_ident.
n:nat
i:combType (Vec Bit n)
(tt, i) = (tt, N2Bv_sized n (Bv2N i * 1))
    rewrite N.mul_1_r, N2Bv_sized_Bv2N.
n:nat
i:combType (Vec Bit n)
(tt, i) = (tt, i)
    reflexivity. }
Qed.

Lemma mul_constN_step n x st i :
  step (mul_constN x) st i = (st, N2Bv_sized n (Bv2N i * x)).
n:nat
x:N
st:circuit_state (mul_constN x)
i:combType (Vec Bit n)
step (mul_constN x) st i =
(st, N2Bv_sized n (Bv2N i * x))
Proof.
n:nat
x:N
st:circuit_state (mul_constN x)
i:combType (Vec Bit n)
step (mul_constN x) st i =
(st, N2Bv_sized n (Bv2N i * x))
  cbv [mul_constN].
n:nat
x:N
st:circuit_state (mul_constN x)
i:combType (Vec Bit n)
step
  match x with
  | 0%N =>
      Comb
        (fun _ : combType (Vec Bit n) =>
         ret (Vec.of_N 0))
  | N.pos p => mul_const_pos p
  end st i = (st, N2Bv_sized n (Bv2N i * x))
  destruct x; [ | apply mul_const_pos_step ].
n:nat
st:circuit_state (mul_constN 0)
i:combType (Vec Bit n)
step
  (Comb
     (fun _ : combType (Vec Bit n) => ret (Vec.of_N 0)))
  st i = (st, N2Bv_sized n (Bv2N i * 0))
  (* remaining case : x = 0 *)
  cbn [step].
n:nat
st:circuit_state (mul_constN 0)
i:combType (Vec Bit n)
(tt, ret (Vec.of_N 0)) =
(st, N2Bv_sized n (Bv2N i * 0)) destruct st.
n:nat
i:combType (Vec Bit n)
(tt, ret (Vec.of_N 0)) =
(tt, N2Bv_sized n (Bv2N i * 0)) simpl_ident.
n:nat
i:combType (Vec Bit n)
(tt, N2Bv_sized n 0) = (tt, N2Bv_sized n (Bv2N i * 0))
  rewrite N.mul_0_r.
n:nat
i:combType (Vec Bit n)
(tt, N2Bv_sized n 0) = (tt, N2Bv_sized n 0) reflexivity.
Qed.